神经网络中复数函数求导

最近接触到了对复数函数的求导，之前已知没有研究过。在看教程的时候，发现自己微积分忘得是一干二净。真的是，233333。算了不多说了，下面对神经网络中的复数函数求导进行记录。

复数神经网络有以下几个特点：

• 网络的输入与权重均为复数
• 损失值为实数

本文的内容主要包含一下几个部分：

• 推导复数神经网络的反向传播公式
• 为复数神经网络的反向传播完成通用代码

Holomorphism与Cauchy-Riemann方程

Holomorphism（全纯）也称为analyticity，维基百科的定义为：

若$U$为$\mathbb{C}$的开子集（开集是指不包含任何自己边界点的集合。或者说，开集包含的任意一点的充分小的邻域都包含在其自身中），且$f:U\to \mathbb{C}$为一个函数。

我们称$f$是在$U$中一点$z_0$是复可微（complex differentiable）或全纯的，当且仅当该极限存在：

$$\begin{array}{}\text{(1)}& f^{\prime }(z_0)=li{m}_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0}\end{array}$$

若$f$在$U$上任取一点均全纯，则称$f$在$U$上全纯。特别地，若函数在整个复平面全纯，我们称这个函数为整函数。

在论文《Deep complex networks》中，是这样定义的（其实和维基百科上定义一致，但是一般英文表述比较严谨，所以放在这里）

Holomorphism, also called analyticity, ensures that a complex-valued function is complex differentiable in the neighborhood of every point in its domain. This means that the derivative, $f^{\prime }(z_0)\equiv li{m}_{\mathrm{\Delta }z\to 0}\frac{f(z_0+\mathrm{\Delta }z)-f(z_0)}{\mathrm{\Delta }z}$of $f$, exists at every point $z_0$ in the domain of $f$ where $f$ is a complex-valued
function of a complex variable $z=x+iy$ such that $f(z)=u(x,y)+iv(x,y)$。$u$和$v$均为实值函数，所以$\mathrm{\Delta }z$可以使用$\mathrm{\Delta }z=\mathrm{\Delta }x+i\mathrm{\Delta }y$ 表达。$\mathrm{\Delta }z$可以从不同的方向逼近0（实轴、虚轴、实轴与虚轴之间）。为了复数可微分，$f^{\prime }(z_0)$不管从哪个方向逼近0，值应该都相同。当$\mathrm{\Delta }z$从实轴逼近0的时候，$f^{\prime }(z_0)$可以写成：

$$\begin{array}{}\text{(2)}& \begin{array}{rlr}{f}^{\prime }(z_0)& \equiv & li{m}_{\mathrm{\Delta }z\to 0}\frac{f(z_0+\mathrm{\Delta }z)-f(z_0)}{\mathrm{\Delta }z}\\ & =& \underset{\mathrm{\Delta }x\to 0}{lim}\underset{\mathrm{\Delta }y\to 0}{lim}\left[\frac{\mathrm{\Delta }u(x_0,y_0)+i\mathrm{\Delta }v(x_0,y_o)}{\mathrm{\Delta }x+i\mathrm{\Delta }y}\right]\\ & =& \underset{\mathrm{\Delta }x\to 0}{lim}\left[\frac{\mathrm{\Delta }u(x_0,y_0)+i\mathrm{\Delta }v(x_0,y_o)}{\mathrm{\Delta }x+i0}\right]\end{array}\end{array}$$

当$\mathrm{\Delta }z$从虚轴逼近0的时候，$f^{\prime }(z_0)$可以写成：

$$\begin{array}{}\text{(3)}& \begin{array}{rlr}{f}^{\prime }(z_0)& \equiv & li{m}_{\mathrm{\Delta }z\to 0}\frac{f(z_0+\mathrm{\Delta }z)-f(z_0)}{\mathrm{\Delta }z}\\ & =& \underset{\mathrm{\Delta }x\to 0}{lim}\underset{\mathrm{\Delta }y\to 0}{lim}\left[\frac{\mathrm{\Delta }u(x_0,y_0)+i\mathrm{\Delta }v(x_0,y_o)}{\mathrm{\Delta }x+i\mathrm{\Delta }y}\right]\\ & =& \underset{\mathrm{\Delta }y\to 0}{lim}\left[\frac{\mathrm{\Delta }u(x_0,y_0)+i\mathrm{\Delta }v(x_0,y_o)}{0+i\mathrm{\Delta }y}\right]\end{array}\end{array}$$

要想使得公式$(2)$和公式$(3)$相等，则需要满足下式：

$$\begin{array}{}\text{(4)}& \frac{\delta f}{\delta z}=\frac{\delta u}{\delta x}+i\frac{\delta v}{\delta x}=-i\frac{\delta u}{\delta y}+\frac{\delta v}{\delta y}\end{array}$$

为了复数可微分，$f$应该满足：

$$\begin{array}{}\text{(5)}& \begin{array}{rlr}\frac{\delta u}{\delta x}& =& \frac{\delta v}{\delta y}\\ \frac{\delta u}{\delta y}& =& -\frac{\delta v}{\delta x}\end{array}\end{array}$$

这被称为Cauchy-Riemann方程（黎曼方程），它是$f$复微分的必要条件。假设$u$和$v$具有连续的一阶偏导数，则Cauchy-Riemann方程成为$f$为Holomorphism的充分条件。

另外，论文中提到Hirose and Yoshida (2012) [1] 证明了对于反向传播，不一定需要函数为Holomorphism，主需要函数关于实部和虚部分别求导即可。

Wirtinger算子

Wirtinger算子的思路是，将任何复变函数$f$，看做$f(z,z^)$，\mathrm{求}\mathrm{导}\mathrm{数}\mathrm{就}\mathrm{是}\mathrm{对}$z$\mathrm{和}\mathrm{共}\mathrm{轭}$z^$分别求导：

$$\begin{array}{}\text{(6)}& df=\frac{\delta f}{\delta z}dz+\frac{\delta f}{\delta z^{\ast }}d{z}^{\ast }\end{array}$$

其中：

$$\begin{array}{}\text{(7)}& \frac{\delta f}{\delta z}=\frac{\delta f}{\delta x}-j\frac{\delta f}{\delta y}\end{array}$$$$\begin{array}{}\text{(8)}& \frac{\delta f}{\delta z^{\ast }}=\frac{\delta f}{\delta x}+j\frac{\delta f}{\delta y}\end{array}$$

复数变量的反向传播

设$J(z)$是定义在复平面$z=x+iy$上的实值损失函数，则根据Wirtinger算子，$J(z)$关于$z$的梯度为：

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathrm{\nabla }J(z)& =\frac{\partial J}{\partial x}+i\frac{\partial J}{\partial y}\\ & =\frac{\partial J}{\partial z}\frac{\partial z}{\partial x}+\frac{\partial J}{\partial z^{\ast }}\frac{\partial z^{\ast }}{\partial x}+i[\frac{\partial J}{\partial z}\frac{\partial z}{\partial y}+\frac{\partial J}{\partial z^{\ast }}\frac{\partial z^{\ast }}{\partial y}]\\ & =2\frac{\partial J}{\partial z^{\ast }}=2{\left(\frac{\partial J}{\partial z}\right)}^{\ast }\end{array}\end{array}$$

在最后一层中，我们使用了实数$J$，对于前面的层只需要一层一层的向前传播即可。

$$\frac{\partial J}{\partial y_l}=\sum _{y_{l+1}}\frac{\partial J}{\partial y_{l+1}}\frac{\partial y_{l+1}}{\partial y_l}+\frac{\partial J}{\partial y_{l+1}^{\ast }}\frac{\partial y_{l+1}^{\ast }}{\partial y_l}.$$

其中$y_l$和$y_{l+1}$分别是第$l$层和第$l+1$的变量；$y_{l+1}=f_l(y_l)$。

复变函数按照是否可导，分为全纯函数holomothic和nonholomophic，判断条件为Cauchy-Riemann方程。

• 如果$f_l$是holomophic（全纯函数），那么上面的第二项消失，变成了：

  $$\frac{\partial J}{\partial y_l}=\sum _{y_{l+1}}\frac{\partial J}{\partial y_{l+1}}\frac{\partial y_{l+1}}{\partial y_l},$$

• 如果$f_l$为nonholomophic

  $$\frac{\partial J}{\partial y_l}=\sum _{y_{l+1}}\frac{\partial J}{\partial y_{l+1}}\frac{\partial y_{l+1}}{\partial y_l}+{\left(\frac{\partial J}{\partial y_{l+1}}\frac{\partial y_{l+1}}{\partial y_l^{\ast }}\right)}^{\ast }.$$

这种思路不同与论文《Deep complex networks》中求导方式，在这种思路中，权重和输入均为复数矩阵，求导时要损失函数对于整个复数求导；而在上述论文中，输入和权重必须可以均为实数（即使用双倍的实数网络代替复数网络），求导时可以分别求实部和虚部的偏导数。

简单测试

给定一个长度为10的向量$x$，网络的损失函数为$J=f_2\left(f_1(f_x(x))\right)$。其中$f_1(z)=z^{\ast }$，$f_2(z)=-e^{-|z{|}^2}$。这是一个简单的方程，naive BP像实数网络会失败，代码在最下面给出：

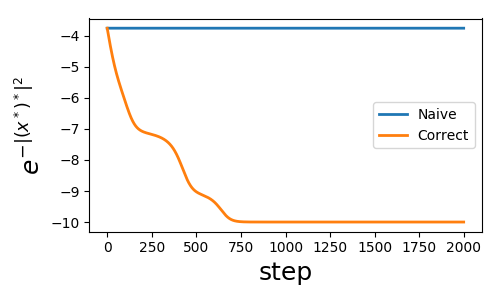
而正确的方程正确的收敛到了-10.

关于复数神经网络的思考

许多计算机科学的人强调复数函数可以使用双倍尺寸的实数网络代替，这是不正确的。这让我们想到一个问题：为什么需要复数值。若没有复数值，那么

• unitary矩阵（酉矩阵）不能很容易的实现
• 相位性质不能很好的表达，光和全息图，声音，量子波函数等

虽然一个复数神经网络必须包含至少一个nonholomophic函数（让损失值为正值）。我认为复数函数的价值在于holomothic，如果一个函数是nonholomophic，那么它和双倍尺寸的复数值网络没有太大区别。

复数神经网络倾向于blow up，那也意味着，不能定义soft函数，像sigmoid和tanh。

代码

'''
Test complex back propagation.
The theory could be found in Akira's book "Complex Valued Neural Networks".
'''

import numpy as np
from matplotlib.pyplot import *

# define two useful functions and their derivatives.
def f1_forward(x): return x.conj()


def df1_z(x, y): return np.zeros_like(x, dtype='complex128')


def df1_zc(x, y): return np.ones_like(x, dtype='complex128')


def f2_forward(x): return -np.exp(-x * x.conj())


def df2_z(x, y): return -y * x.conj()


def df2_zc(x, y): return -y * x

# we compare the correct and incorrect back propagation
def naive_backward(df_z, df_zc):
    '''
    naive back propagation meta formula,
    df_z and df_zc are dirivatives about variables and variables' conjugate.
    '''
    return lambda x, y, dy: df_z(x, y) * dy


def correct_backward(df_z, df_zc):
    '''the correct version.'''
    return lambda x, y, dy: df_z(x, y) * dy +\
                    df_zc(x, y).conj() * dy.conj()


# the version in naive bp
f1_backward_naive = naive_backward(df1_z, df1_zc)
f2_backward_naive = naive_backward(df2_z, df2_zc)

# the correct backward propagation
f1_backward_correct = correct_backward(df1_z, df1_zc)
f2_backward_correct = correct_backward(df2_z, df2_zc)

# initial parameters, and network parameters
num_input = 10
a0 = np.random.randn(num_input) + 1j * np.random.randn(num_input)
num_layers = 3


def forward(x):
    '''forward pass'''
    yl = [x]
    for i in range(num_layers):
        if i == num_layers - 1:
            x = f2_forward(x)
        else:
            x = f1_forward(x)
        yl.append(x)
    return yl


def backward(yl, version):  # version = 'correct' or 'naive'
    '''
    back propagation, yl is a list of outputs.
    '''
    dy = 1 * np.ones(num_input, dtype='complex128')
    for i in range(num_layers):
        y = yl[num_layers - i]
        x = yl[num_layers - i - 1]
        if i == 0:
            dy = eval('f2_backward_%s' % version)(x, y, dy)
        else:
            dy = eval('f1_backward_%s' % version)(x, y, dy)
    return dy.conj() if version == 'correct' else dy


def optimize_run(version, alpha=0.1):
    '''simple optimization for target loss function.'''
    cost_histo = []
    x = a0.copy()
    num_run = 2000
    for i in range(num_run):
        yl = forward(x)
        g_a = backward(yl, version)
        x[:num_input] = (x - alpha * g_a)[:num_input]
        cost_histo.append(yl[-1].sum().real)
    return np.array(cost_histo)


if __name__ == '__main__':
    lr = 0.01
    cost_r = optimize_run('naive', lr)
    cost_a = optimize_run('correct', lr)
    figure(figsize=(5,3))
    plot(cost_r, lw=2)
    plot(cost_a, lw=2)
    legend(['Naive', 'Correct'])
    ylabel(r'$e^{-|(x^*)^*|^2}$', fontsize = 18)
    xlabel('step', fontsize = 18)
    tight_layout()
    show()

复数神经网络

根据我查的资料，这里的复数神经网络并没有用到反向传播中的复数求导机制，而是将复数的实数部分和虚数部分分开拆成两部分进行运算，个人感觉就是上面博客中所说的使用双倍尺寸的实数网络代替复数神经网络，通过下面这一张图可以知道大概原理：

参考

[1] Akira Hirose and Shotaro Yoshida. Generalization characteristics of complex-valued feedforward neural networks in relation to signal coherence. IEEE Transactions on Neural Networks and learning systems, 23(4):
541–551, 2012.

Back Propagation for Complex Valued Neural Networks
【原创】复数神经网络的反向传播算法，及pytorch实现方法
全纯函数