PCA

最近学到了PCA，看到了斯坦福大学的教程，特翻译了一下，并加上了一些自己的理解。

主成分分析（PCA）是用来提升无监督特征学习速度的数据降维算法。

假设你正在训练图像，因为图像中相邻图片的元素具有很高的相关性，所以数据是冗余的。假设输入是16x16的灰度图片，则$\textstyle x \in \Re^{256}$。因为相邻元素之间有很高的关联性，所以PCA可以在错误率很小的情况下对数据进行降维。

例子和数学背景

我们使用$n=2$维度的数据$\textstyle \{x^{(1)}, x^{(2)}, \ldots, x^{(m)}\}$作为输入，则$\textstyle x^{(i)} \in \Re^2$。为了方便解释，我们以二维数据降一维为例（实际应用可能需要把数据从256维降到50维）：

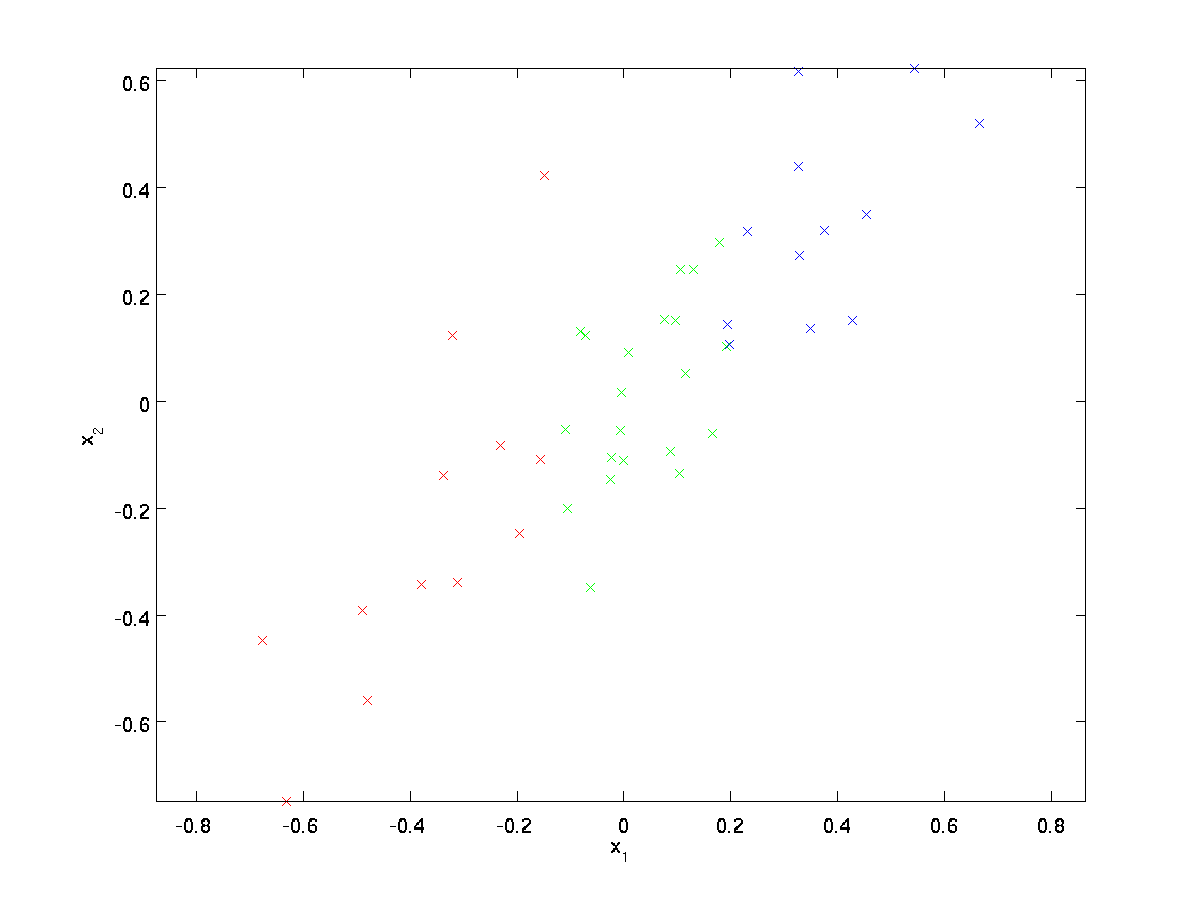
这里的对数据降维指的是降低数据的维度，而不是减少数据的数目。

在上图中数据已经经过归一化处理，特征值$x_1$和$x_2$拥有相同的均值(0)和方差。根据坐标的不同将上面数据使用三种颜色表示出来(颜色与算法无关)。PCA找到一个低维空间将数据进行投影。

通过上图点的可视化，可以发现，$u_1$是数据的主要变化方向，而$u_2$是数据的次要变化方向。

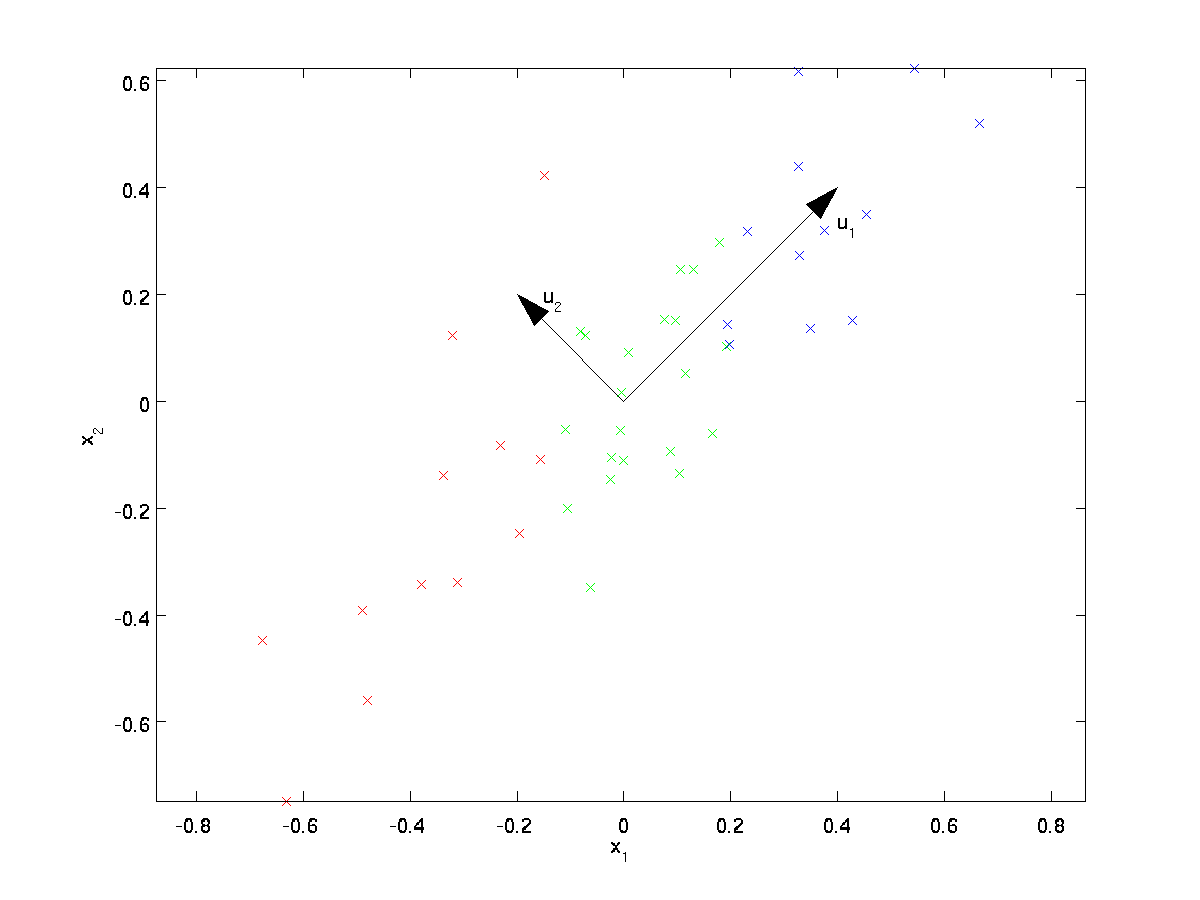
也就是说，数据在$u_1$方向的变化幅度要大于在$u_2$方向的变化幅度。更正式的找到$u_1$和$u_2$，首先计算下面的矩阵$\textstyle \Sigma$：

$$\begin{align} \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T. \end{align}$$

$x^{i}$为列向量。如果$x$的均值为零，则$\textstyle \Sigma$是$x$的协方差矩阵(这解释了上面的数据为什么要进行归一化)。注意这里的$\textstyle \Sigma$是标准的协方差表示方法，而不是求和$\sum_{i=1}^n i$。

方差是同一类或者说同一维数据的离散性，而协方差则是不同维度数据的相关性，协方差为0说明二者独立不相关，为负就是负相关，为正就是正相关）。协方差的公式为：

$$conv(x,y)=\frac {\sum_{i=1}^m({x_i-\overline{x}})({y_i-\overline{y}})}{m-1}$$

可以证明数据变化的主方向$u_1$就是协方差矩阵的主特征向量(主特征值对应的特征向量为主特征向量，而主特征值是指模最大（如果是实数的话就是绝对值最大）的特征值)，而$u_2$就是次特征向量（原理有兴趣的同学请看这里）。

您可以使用标准的数值线性代数软件来查找这些特征向量(参见实现说明)。具体来说，让我们计算$\textstyle \Sigma$(即协方差矩阵)的特征向量，并将这些特征向量叠加在列中，形成矩阵$U$：

$$\begin{align} U = \begin{bmatrix} | & | & & | \\ u_1 & u_2 & \cdots & u_n \\ | & | & & | \end{bmatrix} \end{align}$$

在上面，$u_1$是主特征向量，而$u_2$是第二特征向量，等等。$\textstyle \lambda_1, \lambda_2, \ldots, \lambda_n$对应上面的特征向量。

矩阵特征向量表达式：$Ax=\lambda x$。

我们可以近似利用向量$u_1$和$u_2$来表示数据。具体来说，让$\textstyle x \in \Re^2$做一些训练，然后$\textstyle u_1^Tx$是$x$在向量$u_1$上投影长度。而$\textstyle u_2^Tx$是$x$在向量$u_2$上投影长度。

对协方差矩阵求特征分解求出特征向量也可以用奇异值分解（SVD）来求解，SVD求解出的U即为协方差矩阵的特征向量。U是变换矩阵或投影矩阵，即为上面说的坐标方向，U的每一列就是一个投影方向。另外具体参考内积的几何意义。

旋转数据

我们将$x$使用$\textstyle (u_1, u_2)$基向量进行表示:

$$\begin{align} x_{\rm rot} = U^Tx = \begin{bmatrix} u_1^Tx \\ u_2^Tx \end{bmatrix} \end{align}$$

对整个训练样本转换，即对于每一个$i$均有$\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}$，画出$\textstyle x_{\rm rot}$的图像

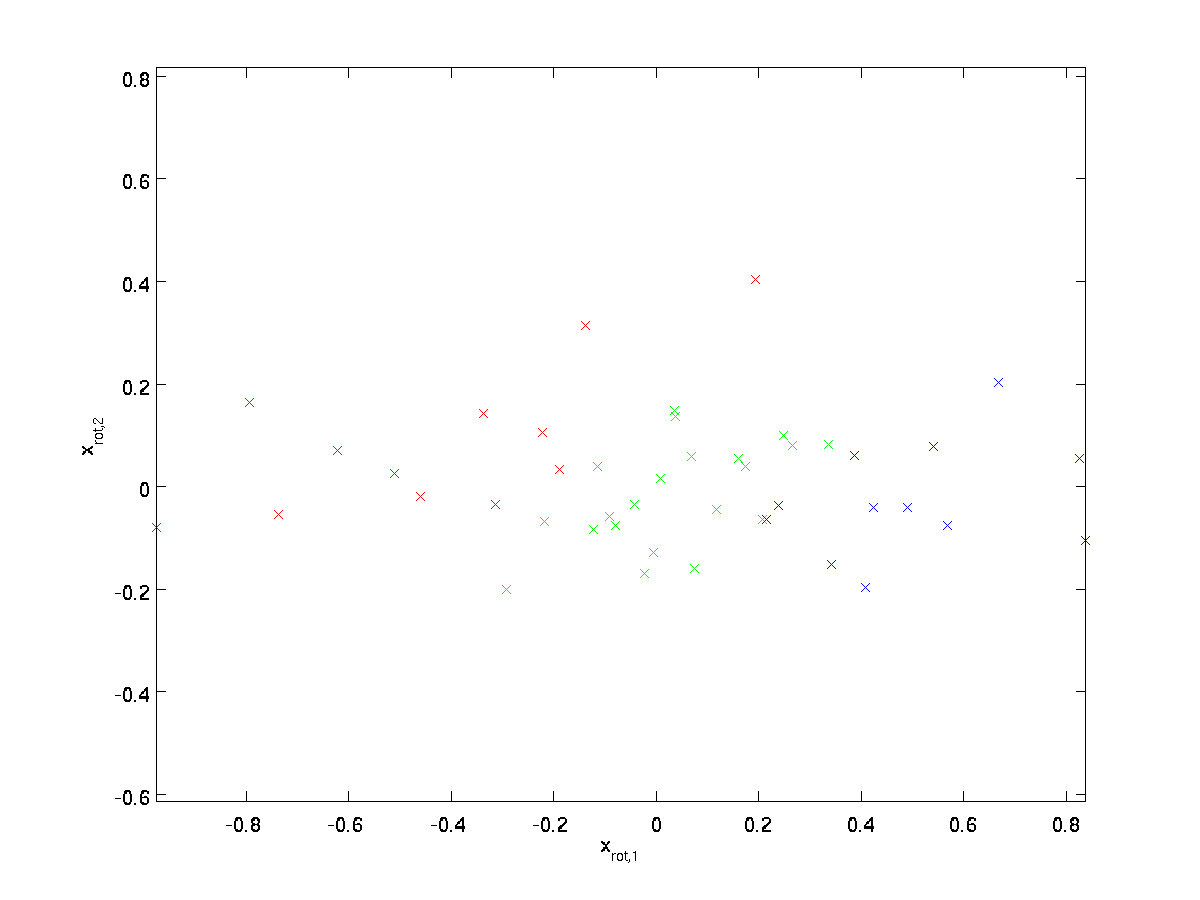
这是训练集在$u_1,u_2$基上的旋转，在更一般的情况下，$\textstyle U^Tx$是旋转到$u_1,u_2,…,u_n$上的训练集。$U$是一个正交矩阵，即$\textstyle U^TU = UU^T = I$。已知$\textstyle x_{\rm rot}$求$x$，可以使用

$$\begin{align} x = U x_{\rm rot} , \end{align}$$

因为$\textstyle U x_{\rm rot} = UU^T x = x$。

数据降维

我们可以看到，数据变化的主要方向是第一维，即这个旋转的数据中的$\textstyle x_{\rm rot,1}$。如果我们想把数据降到一维，则

$$\begin{align} \tilde{x}^{(i)} = x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)} \in \Re. \end{align}$$

更一般情况下，如果$\textstyle x \in \Re^n$，我们想减少至$k$维，即$\textstyle \tilde{x} \in \Re^k$，其中$k<n$。我们取$\textstyle x_{\rm rot}$的前$k$个部分，这对应于变化的前$k$个方向。

另外一种PCA的解释为$\textstyle x_{\rm rot}$是一个$n$维向量，前几个元素可能特别大(例如，对于大多数的样本$i$而言，$\textstyle x_{\rm rot,1}^{(i)} = u_1^Tx^{(i)}$取得了相当大的值)。后面的元素可能特别小(例如，$\textstyle x_{\rm rot,2}^{(i)} = u_2^Tx^{(i)}$更有可能是小的)。PCA将$\textstyle x_{\rm rot}$的后面(小的)元素丢弃掉，将他们近似为零向量。具体来说，我们可以除了前$k$个元素，其余均为零元素的$\textstyle x_{\rm rot}$去近似得到$\textstyle \tilde{x}$。公式如下:

$$\begin{align} \tilde{x} = \begin{bmatrix} x_{\rm rot,1} \\ \vdots \\ x_{\rm rot,k} \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \approx \begin{bmatrix} x_{\rm rot,1} \\ \vdots \\ x_{\rm rot,k} \\ x_{\rm rot,k+1} \\ \vdots \\ x_{\rm rot,n} \end{bmatrix} = x_{\rm rot} \end{align}$$

在我们的例子中，$\textstyle \tilde{x}$的图如下($\textstyle n=2, k=1$)

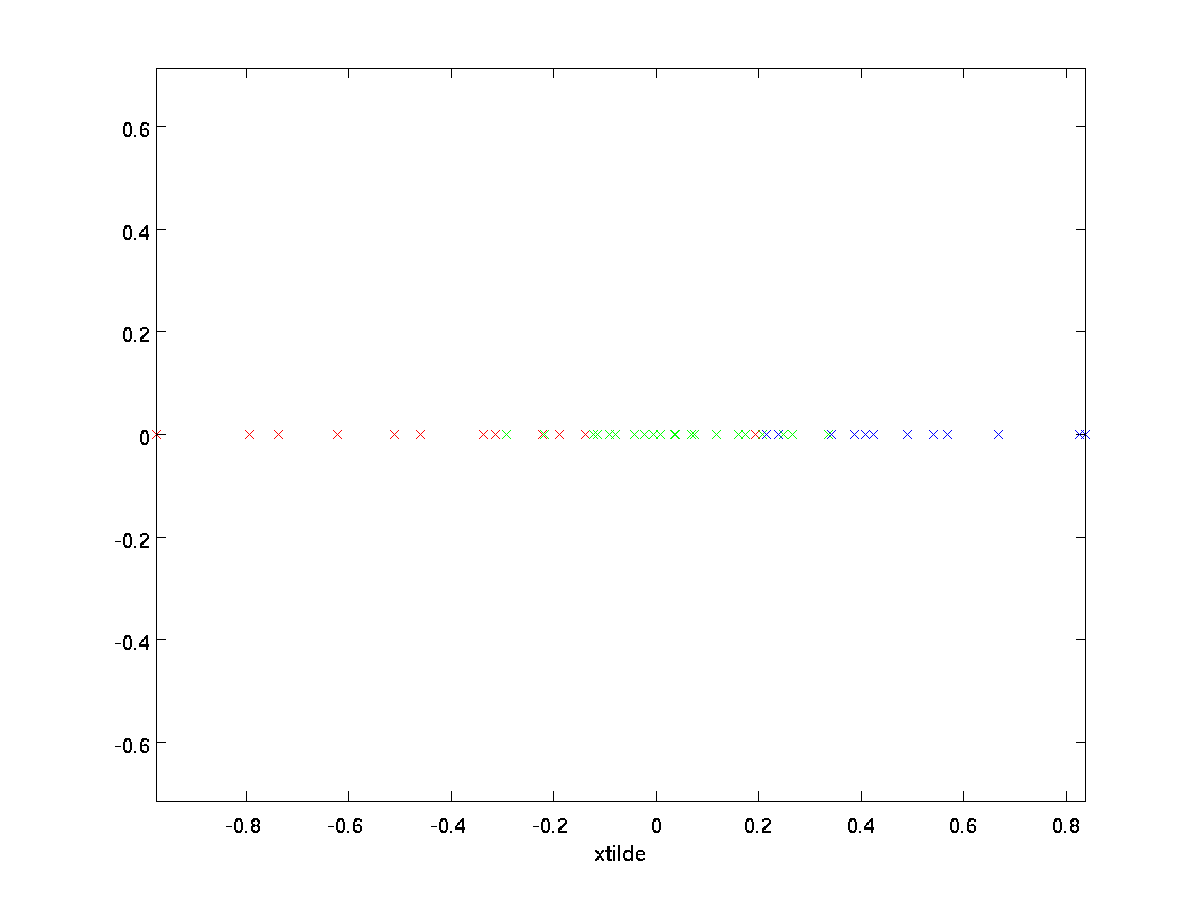
上面的$\textstyle \tilde{x}$中的$n-k$个元素均为零，我们可以省略掉零元素，使得$\textstyle \tilde{x}$为$k$维数据。

这也解释了为什么我们要在$\textstyle u_1, u_2, \ldots, u_n$基向量上表示我们的数据：决定保留哪$k$个元素。通过这些操作，我们可以说保留了前$k$个PCA(主)成分。

数据的复原

现在$\textstyle \tilde{x} \in \Re^k$是原始数据$\textstyle x \in \Re^n$的低维、压缩表示。之前，我们说过$\textstyle x = U x_{\rm rot}$。$\textstyle \tilde{x}$是$\textstyle x_{\rm rot}$的一种近似。因为$\textstyle \tilde{x} \in \Re^k$，我们对$\textstyle \tilde{x}$补$n-k$个零得到$\textstyle x_{\rm rot} \in \Re^n$的近似。最后，乘上$U$即可得到$x$的近似。

$$\begin{align} \hat{x} = U \begin{bmatrix} \tilde{x}_1 \\ \vdots \\ \tilde{x}_k \\ 0 \\ \vdots \\ 0 \end{bmatrix} = \sum_{i=1}^k u_i \tilde{x}_i. \end{align}$$

上面$u_1,u_2,…,u_n$是列向量。

上面的$U$来自前面的定义。实际中，我们并不是真的对$\textstyle \tilde{x}$补零再乘以$U$，因为这将导致零乘。实际上，我们只需要用$U$的前$k$列乘以$\textstyle \tilde{x} \in \Re^k$。

右乘$\textstyle \tilde{x}$相当于对$U$中各列进行线性组合，系数为$\textstyle \tilde{x}$中各个值。

对于我们的数据，$\textstyle \hat{x}$的示意图如下

因此，我们可以使用一维去近似我们的原始数据。

如果你正在训练自动编码器或其他无监督的特征学习算法，你的算法的运行时间将取决于输入的维数。如果使用$\textstyle \tilde{x} \in \Re^k$去代替$x$，然后，你将对低维数据进行训练，因此你的算法可能会运行得更快。对于许多数据集，低维$\textstyle \tilde{x}$表示可以非常好地逼近原始数据，使用PCA这种方法可以显著提高算法的速度，同时引入非常小的逼近误差。

保留的元素个数

我们如何决定$k$呢，如果$k$比较大的话，那么数据无法得到很大的压缩，极端情况下若$k=n$，我们就是在使用原始数据(经过了在不同基向量上变换)。若$k$比较小，那么我们可能使用了一个非常糟糕的数据近似值。

为了决定如何设置$k$，我们通常会查看不同k值的“保留方差百分比”，具体来说，如果$k=n$，那么我们就得到了数据的精确近似值，我们说100%的保留方差。即原始数据的所有变化都被保留。相反，如果$k=0$，那么我们用0向量逼近所有数据，这样方差就保留了0%。

更普遍，$\textstyle \lambda_1, \lambda_2, \ldots, \lambda_n$是的$\textstyle \Sigma$的特征值(降序排序)，因此$\textstyle \lambda_j$相对应的特征值特征向量$u_j$。

如果保留$k$个主成分，保留的方差百分比由下式给出：

$$\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j}. \end{align}$$

在上面的例子中，$\textstyle \lambda_1 = 7.29$而$\textstyle \lambda_2 = 0.69$。因此，通过只保留$k=1$个主成分，我们保留了$7.29/(7.29+0.69)=0.913$，即91.3%的方差。

对于图像，一种常见的启发式方法是选择$k$，从而保留99%的方差。换句话说，我们选择满足$k$的最小值。

$$\begin{align} \frac{\sum_{j=1}^k \lambda_j}{\sum_{j=1}^n \lambda_j} \geq 0.99. \end{align}$$

根据应用程序的不同，如果您愿意容忍一些额外的错误，有时也会使用90-98%范围内的值。当你向其他人描述如何应用PCA时，说选择$k$来保留95%的方差也比说保留了120个(或任何其他数量的)分量要容易得多。

图像上的PCA

要使PCA正常工作，通常需要每个特性$\textstyle x_1, x_2, \ldots, x_n$具有与其他值类似的值范围(并具有接近于零的平均值)。如果你以前在其他应用程序中使用过PCA，那么你可能会分别对每个特征进行预处理，使其具有零均值和单位方差，方法是分别估计每个特征$\textstyle x_j$的均值和方差。在大多数图像中，不能采用这种预处理方式。更具体的说，假设我们在自然图像上训练我们的算法，那么$\textstyle x_j$是每个像素$j$的值。

在对自然图像进行训练时，估计每个像素的单独均值和方差没有多大意义，因为图像一部分的统计数据(理论上)应该与其他任何部分相同。

图像的这种性质称为“平稳性”。

具体而言，为了使PCA更好地工作，我们非正式地要求：(i)各特征的均值近似为零；(ii)不同特征之间具有类似的方差。对于自然图像，即使没有方差归一化，(ii)也已经满足，因此我们将不进行任何方差归一化。(如果使用音频数据(例如，光谱图)或文本数据(例如，字包向量)等进行训练，我们通常也不会进行方差归一化。)

事实上，PCA对数据的缩放是不变的，并且无论输入的缩放大小如何，它都会返回相同的特征向量。更正式地说，如果将每个特征向量$x$乘以某个正数(从而将每个训练样本中的每个特征按相同的比例缩放)，PCA的输出特征向量将不会改变。

所以，我们不会使用方差规划化，只需对均值进行规范化，确保每一个特征都是零均值。在应用中，我们经常对图像的亮度不感兴趣。例如，在物体回归问题中，图像的总体亮度不会影像物体的位置。更正式，我们对一个图像块的平均强度值不感兴趣。因此我们可以减去这个值，这是归一化的一种形式。

具体的，如果$\textstyle x^{(i)} \in \Re^{n}$是16x16图像块(n=256)的亮度值(灰度图)，我们可能对每一个图像$\textstyle x^{(i)}$的亮度进行规范化，对于每一个$j$：

$$\mu^{(i)} := \frac{1}{n} \sum_{j=1}^n x^{(i)}_j \\ x^{(i)}_j := x^{(i)}_j - \mu^{(i)}$$

注意对于每个图像$x^(i)$都有两个步骤，并且$\textstyle \mu^{(i)}$是图像$x^(i)$的亮度均值。这与单独估计每个像素$x_j$的平均值是不同的。

如果你正在对自然图像以外的图像(例如手写字符的图像或以白色背景为中心的单个孤立对象的图像)进行算法训练，则其他类型的规范化可能值得考虑，而最佳选择可能取决于应用场景。但是，在自然图像训练中，使用上述公式中给出的每幅图像的均值归一化方法将是一个合理的缺省值。

白化

我们使用PCA降低数据的维数。有一个密切相关的预处理步骤叫白化(也称为球化)。如果我们对图像进行训练，原始输入是有多余的项，因为相邻的像素值高度相关。白化的目标是减少输入的冗余；更正式地说，期望我们的学习算法得到一个训练输入，满足(i)特征之间的相关性较小，(ii)所有特征都具有相同的方差。

二维的例子

我们首先使用之前的2D例子描述白化。然后我们将描述如何将平滑与其相结合，以及如何将PCA与其相结合。

如何使得输入特征之间互相不相关呢？我们计算$\textstyle x_{\rm rot}^{(i)} = U^Tx^{(i)}$时已经实现了这个。把我们之前的图再画出来，$\textstyle x_{\rm rot}$如图所示：

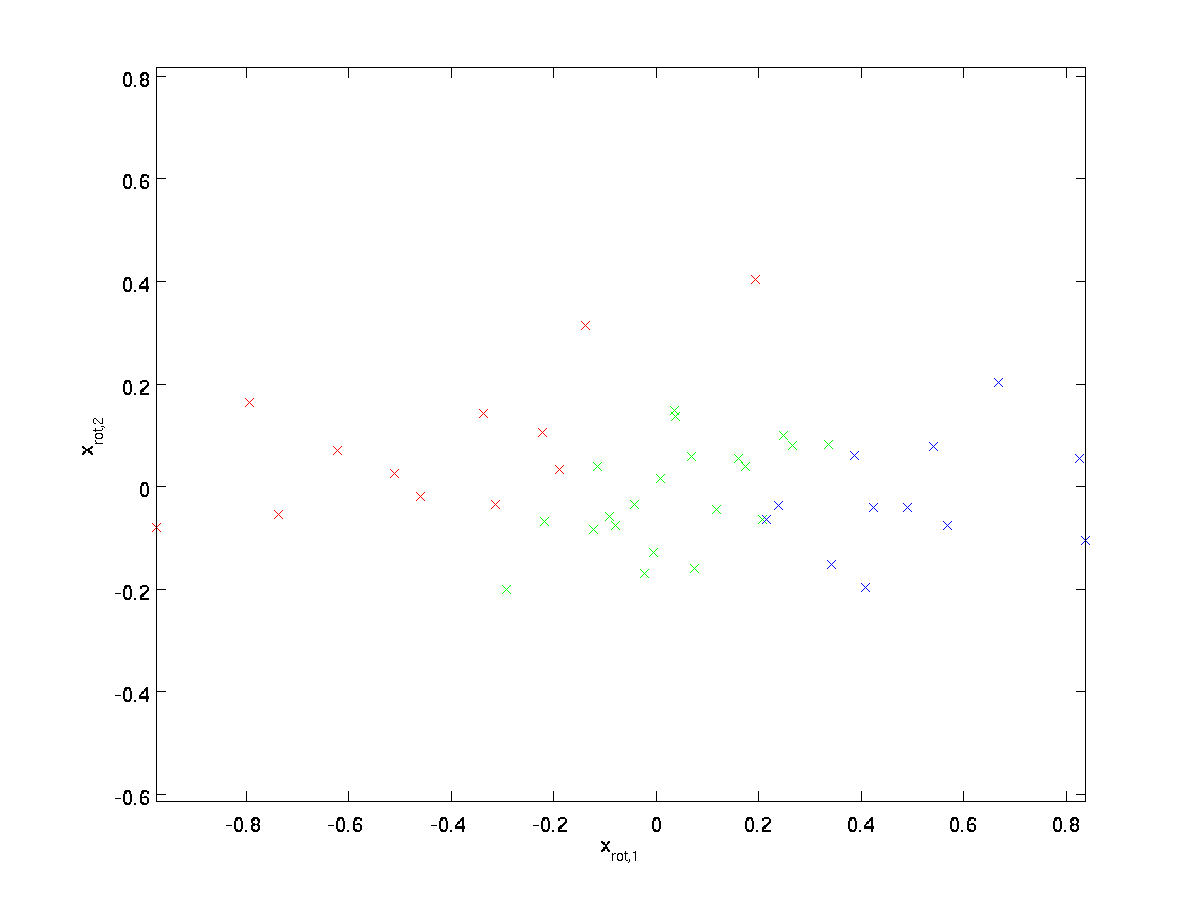
？？？这个数据的协方差矩阵为：

$$\begin{align} \begin{bmatrix} 7.29 & 0 \\ 0 & 0.69 \end{bmatrix}. \end{align}$$

(注：从技术上讲，本节中关于“协方差”的许多陈述只有在数据均值为零的情况下才是正确的。在本节的其余部分，我们将把这一假设视为隐含在我们的声明中。然而，即使数据的均值不完全为零，我们这里给出的直觉仍然成立，因此这不是你应该担心的事情。)

对角元素为$\textstyle \lambda_1$和$\textstyle \lambda_2$。且非对角线上的元素为零，因此，$\textstyle x_{\rm rot,1}$和$\textstyle x_{\rm rot,2}$是不相关的。满足我们对白化数据的需求之一(即特征之间的相关性较低)。

为了使我们的每个输入特性具有单位方差，我们可以每个特征$\textstyle x_{\rm rot,i}$除以$\textstyle 1/\sqrt{\lambda_i}$进行调整。具体而言，我们定义白化数据$\textstyle x_{\rm PCAwhite} \in \Re^n$为下面形式：

$$\begin{align} x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}. \end{align}$$

画出$\textstyle x_{\rm PCAwhite}$，我们得到下图

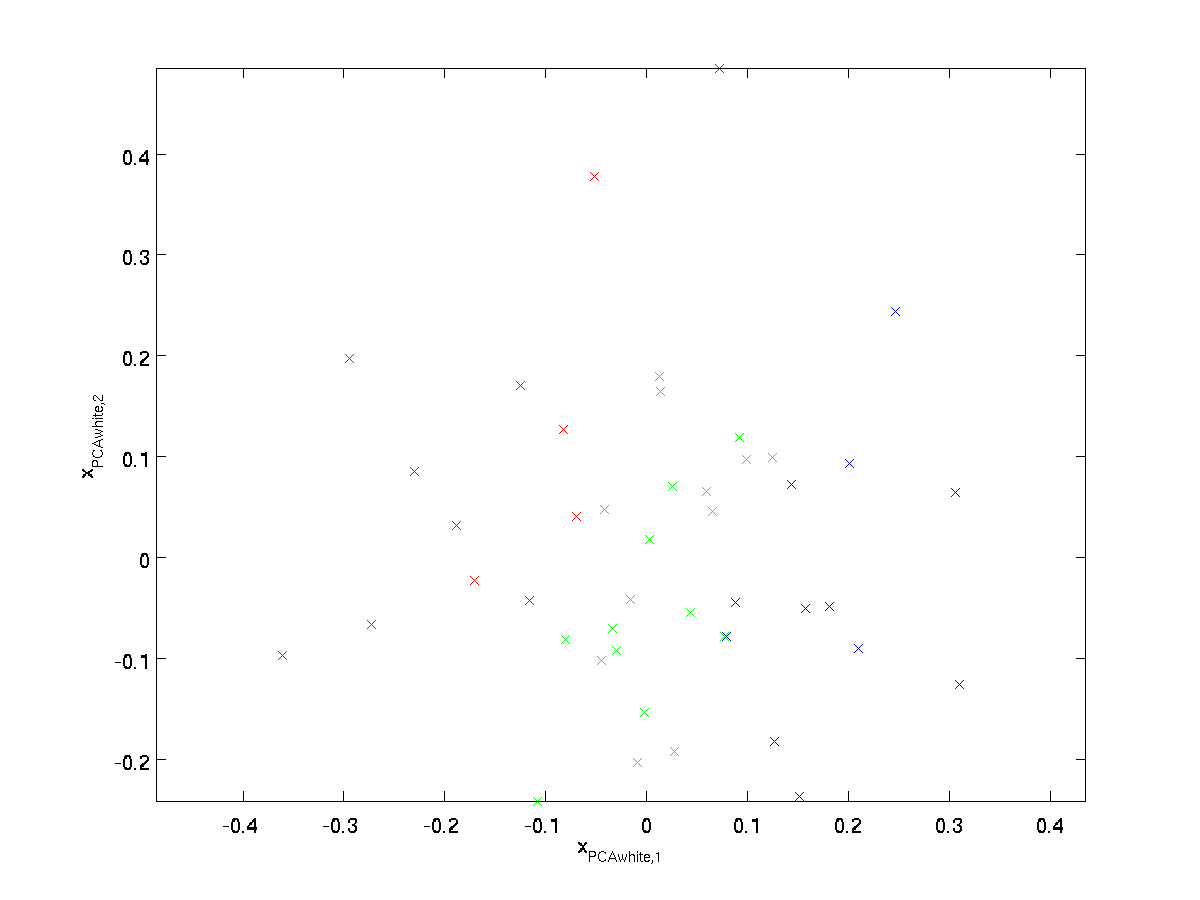
这个数据的方差现在等于单位阵$\textstyle I$，称$\textstyle x_{\rm PCAwhite}$PCA白化版本：$\textstyle x_{\rm PCAwhite}$的不同元素之间是不相关的并且有单位方差。

白化与降维相结合。如果你希望数据被白化，并且比原始输入的维数更低，那么您还可以选择只保留$\textstyle x_{\rm PCAwhite}$的前k项。当我们将PCA白化和正则化结合起来时(稍后将介绍)，$\textstyle x_{\rm PCAwhite}$的最后几项无论如何都将接近于零，因此可以安全地丢弃。

ZCA白化

最后，事实证明这种让数据具有协方差恒等式$I$的方法并不是唯一的。具体地说，如果$R$是任意正交矩阵，使得$R$满足$\textstyle RR^T = R^TR = I$(如果$R$是旋转/反射矩阵)，那么$\textstyle R \,x_{\rm PCAwhite}$也将具有恒等协方差。

在ZCA白化中，我们选择$\textstyle R = U$，我们定义

$$\begin{align} x_{\rm ZCAwhite} = U x_{\rm PCAwhite} \end{align}$$

我们画出来$\textstyle x_{\rm ZCAwhite}$，得到下图

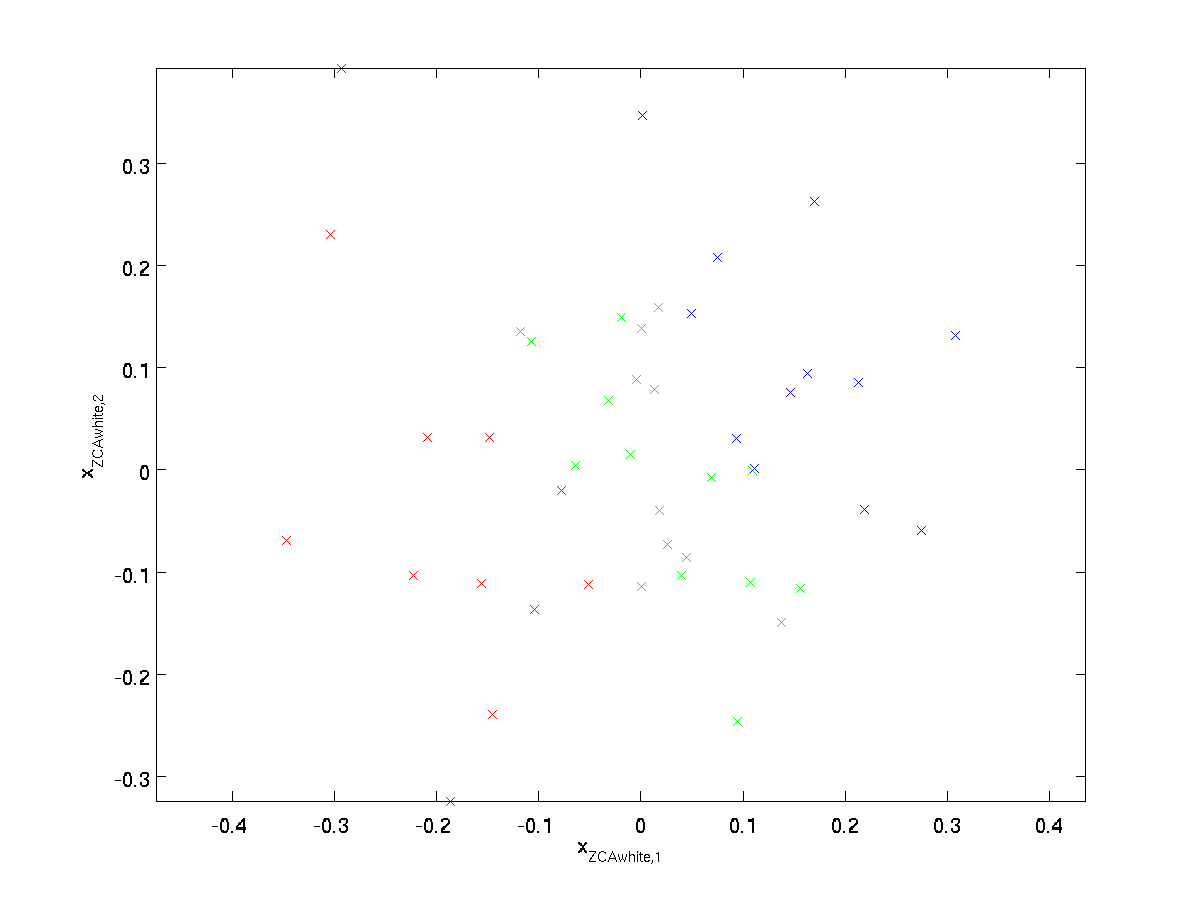
可以看出，在$R$的所有可能选择中，这种旋转使得$\textstyle x_{\rm ZCAwhite}$尽可能接近原始输入数据$x$。

当使用ZCA白化的时候(不同于PCA白化)，我们通常保留数据所有的维度，不会降低维度。

正则化

无论是PCA白化还是ZCA白化，有时一些特征值$\textstyle \lambda_i$接近零。当放缩的时候，我们会除以$\sqrt{\lambda_i}$，会除以一个接近零的值。这可能会导致数据爆炸(取很大的值)，或者在数值上不稳定。因此，在实践中，我们使用少量的正则化来实现这个缩放步骤，并在特征值取平方根和求逆之前向特征值添加一个小的常量$\textstyle \epsilon$：

$$\begin{align} x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i + \epsilon}}. \end{align}$$

当$x$的取值范围在$[-1,1]$之间的时候，可以取$\textstyle \epsilon \approx 10^{-5}$。

对于图像，在这里添加$\textstyle \epsilon$也有稍微平滑(或低通滤波)输入图像的效果。这也有一个理想的效果，消除由图像中像素布局方式引起的混叠伪影，并可以改进所学习的特性(细节超出了这些注释的范围)。

ZCA白化是将数据$x$映射到$\textstyle x_{\rm ZCAwhite}$的一种预处理方式。事实证明，这也是生物眼(视网膜)处理图像的粗略模型。具体来说，当你的眼睛感知图像时，你眼睛中大多数相邻的“像素”都会感觉到非常相似的值，因为图像的相邻部分在强度上往往是高度相关的。因此，你的眼睛必须将每个像素分别传输(通过你的视神经)到你的大脑，这是浪费的。相反，你的视网膜执行去关联操作(这是通过视网膜神经元来完成的，这些神经元计算一个被称为“上中心，外环绕声中心，上环绕声”的功能)，这类似于ZCA所做的操作。这将减少输入图像的冗余表示，然后将输入图像传输到您的大脑。

PCA白化实现

在这一节中，我们总结了PCA、PCA白化和ZCA白化算法，并描述了如何使用有效的线性代数库来实现它们。

首先，我们需要确保数据具有(近似)零均值。

对于自然图像，我们(近似)通过减去每个图像块的平均值来实现这一点。我们通过减去每个图像块的平均值来实现这一点。在Matlab中，我们可以通过使用：

avg = mean(x, 1); % Compute the mean pixel intensity value separately for each patch. 
x = x - repmat(avg, size(x, 1), 1);

接着，我们计算$\textstyle \Sigma = \frac{1}{m} \sum_{i=1}^m (x^{(i)})(x^{(i)})^T$，如果您是在Matlab中实现此功能(或者即使您是在C+、Java等语言中实现此功能，但可以访问有效的线性代数库)，则以显式和的形式执行此操作是低效的。相反，我们可以一次性计算出：

sigma = x * x' / size(x, 2);

这里，$x$是一个$nxm$的矩阵，每一列均是一个样本。

接着，PCA需要计算协方差$\Sigma$的特征向量。可以使用Matlab的eig函数完成此操作。然而，由于$\Sigma$是一个对称的半正定矩阵，使用svd函数在数值上更可靠。

[U,S,V] = svd(sigma);

矩阵$U$将包含$\Sigma$的主向量(每列一个特征向量，按主次特征向量排序)，矩阵$S$的对角项将包含相应的特征值(也按递减顺序排序)。矩阵$V$等于矩阵$U$，可以安全的忽略。

注：svd函数实际上计算矩阵的奇异向量和奇异值，对于对称半正定矩阵的特殊情况，这就是我们在这里所关注的，等于它的特征向量和特征值。(对奇异向量与特征向量的全面讨论超出了本文的讨论范围。)

最后，计算$x_{rot}$和$\textstyle \tilde{x}$：

xRot = U' * x; % rotated version of the data. 
xTilde = U(:,1:k)' * x; % reduced dimension representation of the data, 
                         % where k is the number of eigenvectors to keep

这将给出$\textstyle \tilde{x} \in \Re^k$的PCA数据表示。

顺便说一句，如果$x$是一个$n×m$矩阵，包含了所有的训练数据，那么这是一个向量化实现，上面的表达式同样适用于计算整个训练集的$x_{\rm rot}$和$\tilde{x}$。得到的$x_{\rm rot}$和$\tilde{x}$将有一列对应于每个训练样本。

计算PCA白化$\textstyle x_{\rm PCAwhite}$，使用

xPCAwhite = diag(1./sqrt(diag(S) + epsilon)) * U' * x;

$S’s$的对角包含特征值$\textstyle \lambda_i$。这是一种简洁的计算同时对于所有的$i$计算$\textstyle x_{\rm PCAwhite,i} = \frac{x_{\rm rot,i} }{\sqrt{\lambda_i}}$的方法。

最后，你也可以计算ZCA白化数据$\textstyle x_{\rm ZCAwhite}$：

xZCAwhite = U * diag(1./sqrt(diag(S) + epsilon)) * U' * x;