指数加权移动平均(Exponential Weighted Moving Average),简写为EMA。最近不知道干点啥,没有目标,所以想着先打好机器学习的基础吧,所以就简单的总结了一下基于梯度的一些优化算法,但是在看到Adadelta算法的时候,碰到了指数加权移动平均,感觉要理解这个算法,必须要理解EMA,所以在网上就抄袭了以下的内容。
为了理解下面的内容,我们先介绍一下什么是指数(妈呀这也能忘,今天高考完了,我这水平去参加高考,估计连二本都够呛了吧,23333~)。
指数是幂运算$aⁿ(a≠0)$中的一个参数,$a$为底数,$n$为指数,指数位于底数的右上角,幂运算表示指数个底数相乘。当$n$是一个正整数,$aⁿ$表示$n$个$a$连乘。当$n=0$时,$aⁿ=1$。
EMA 简介
演化
算术平均(权重相等)—>加权平均(权重不等)—>移动平均(大约是只取最近的 N 次数据进行计算)—> 批量归一化(BN)及各种优化算法的基础。
EMA:是以指数式递减加权的移动平均,各数值的加权影响力随时间呈指数式递减,时间越靠近当前时刻的数据加权影响力越大。
公式及理解
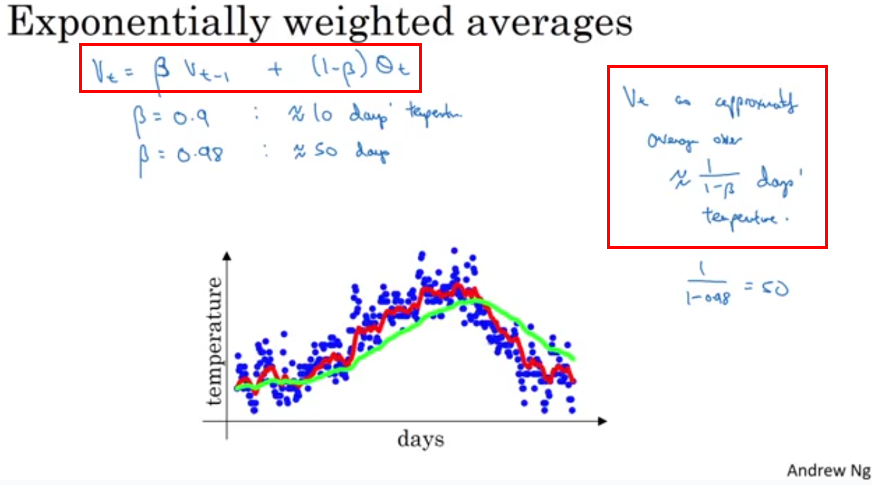
$v_t = \beta v_{t-1} + (1 - \beta)\theta_{t}$,公式中$\theta_t$为$t$时刻的实际温度;系数$β$表示加权下降的快慢,值越小权重下降的越快;$v_t$为$t$时刻 EMA 的值。
当$v_0 = 0$的时候,可得$v_t = (1-\beta) (\theta_{t}+\beta\theta_{t-1}+\beta^{2}\theta_{t-2}+ … +\beta^{t-1}\theta_{1})$,从公式中可以看到:每天温度$(θ)$的权重系数以指数等比形式缩小,时间越靠近当前时刻的数据加权影响力越大。
在优化算法中,我们一般取$\beta >= 0.9$,而$1 + \beta + \beta^{2} + … + \beta^{t-1} = \frac{1-\beta^{t}}{1-\beta}$,所以当 t 足够大时$\beta^{t} \approx 0$,此时便是严格意义上的指数加权移动平均。

在优化算法中,我们一般取$\beta >= 0.9$,此时有$\beta^{\frac{1}{1-\beta}} \approx \frac{1}{e} \approx 0.36$,也就是说$N = \frac{1}{1-\beta}$天后,曲线的高度下降到了约原来的$\frac{1}{e}$。由于时间越往前推移 $θ $权重越来越小,所以相当于说:我们每次只考虑最近(latest) $N = \frac{1}{1-\beta}$天的数据来计算当前时刻的 EMA,这也就是移动平均的来源。
EMA 偏差修正
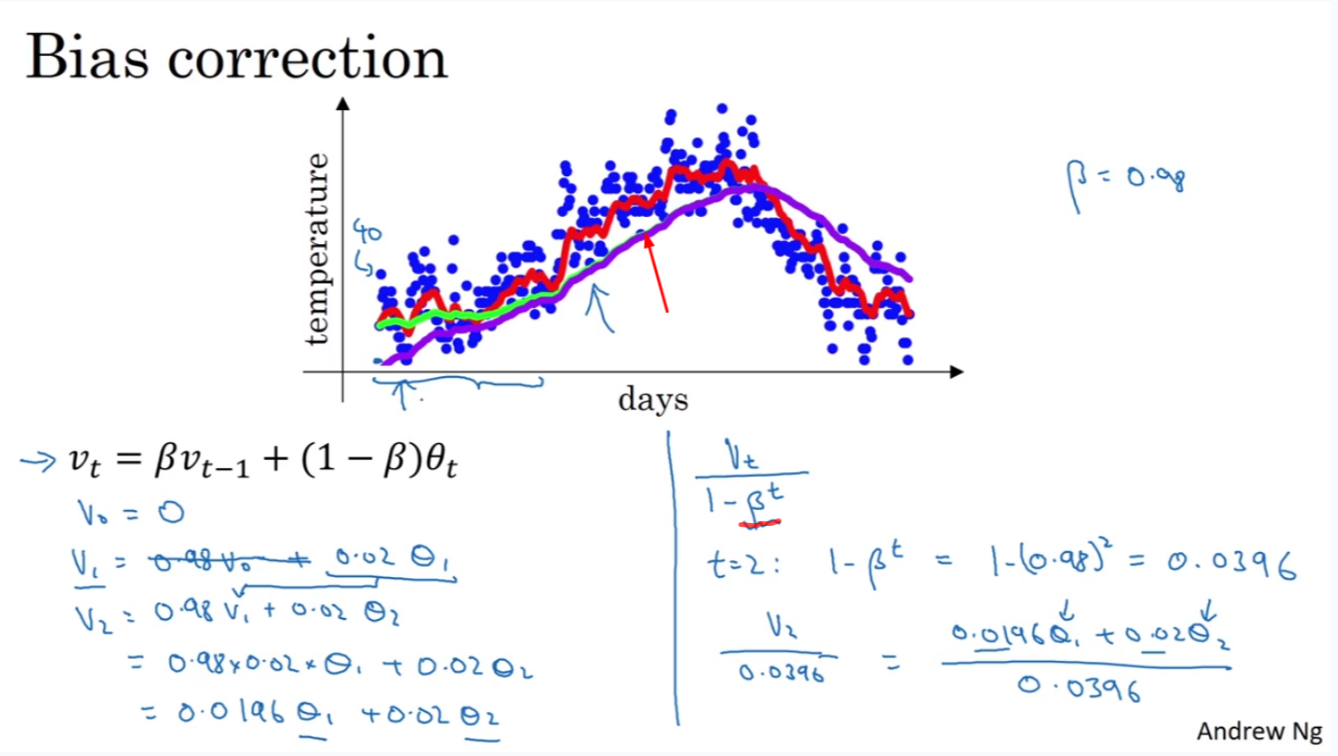
在$\beta = 0.98$时,理想状况下,我们应该能得到绿色曲线,然而现实我们得到的却是紫色曲线,它的起点比真实的要低很多,不能很好的估计起始位置的温度,此问题称为:冷启动问题,这是由于$ v_0=0 $造成的。
解决方案:将所有时刻的 EMA 除以$1 - \beta^{t}$后作为修正后的 EMA。当 $t$很小时,这种做法可以在起始阶段的估计更加准确;当 $t $很大时,偏差修正几乎没有作用,所以对原来的式子几乎没有影响。注意:我们一般取$\beta >= 0.9$,计算 $t $时刻偏修正后的 EMA 时,用的还是$ t−1$时刻修正前的EMA。
EMA 的优点及其应用理解
EMA 的优点
它占用极少内存:计算指数加权平均数只占用单行数字的存储和内存,然后把最新数据代入公式,不断覆盖就可以了。
移动平均线能较好的反应时间序列的变化趋势,权重的大小不同起到的作用也是不同,时间比较久远的变量值的影响力相对较低,时间比较近的变量值的影响力相对较高。
EMA 在 Momentum 优化算法中应用的理解
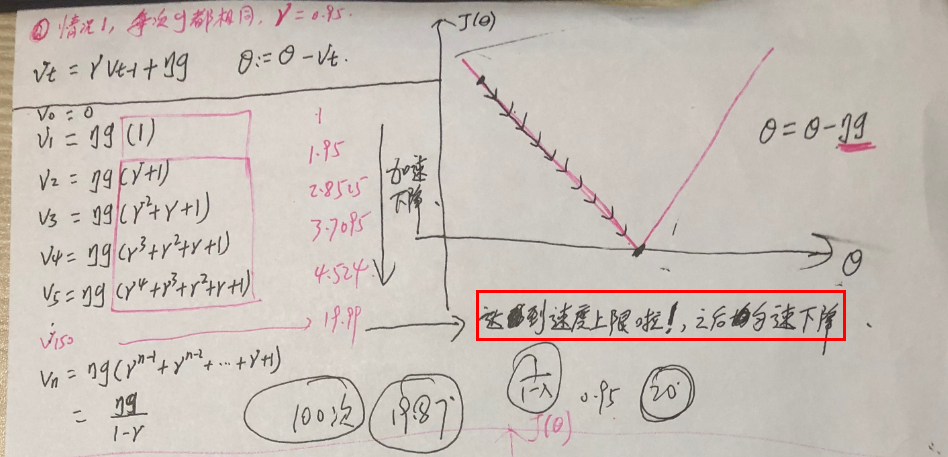
假设每次梯度的值都是$\gamma = 0.95$ ,此时参数更新幅度会加速下降,当 $n$ 达到 150 左右,此时达到了速度上限,之后将匀速下降(可参考一中的公式理解)。
假如,在某个时间段内一些参数的梯度方向与之前的不一致时,那么真实的参数更新幅度会变小;相反,若在某个时间段内的参数的梯度方向都一致,那么其真实的参数更新幅度会变大,起到加速收敛的作用。在迭代后期,由于随机噪声问题,经常会在收敛值附近震荡,动量法会起到减速作用,增加稳定性。
参考
Coursera:Exponentially-Weighted-Moving-Averages
指数
指数加权移动平均(Exponential Weighted Moving Average)

